05  Suites numériques

Des suites de nombres 2 4 6 8 16... ou 4000 2000 1000 500... vous en avez croisées dès l'école primaire.

Vous deviez trouver les nombres manquants.
En Première, leur étude ira un peu plus loin. On devra par exemple trouver directement le centième ou le millième terme d'une suite ou alors décrire son comportement, c'est-à-dire:
- ses variations: est-ce que la suite est croissante, décroissante, oscille-t-elle?
- sa limite: si on calcule des termes de la suite "pendant très longtemps", que peut-on prévoir ?

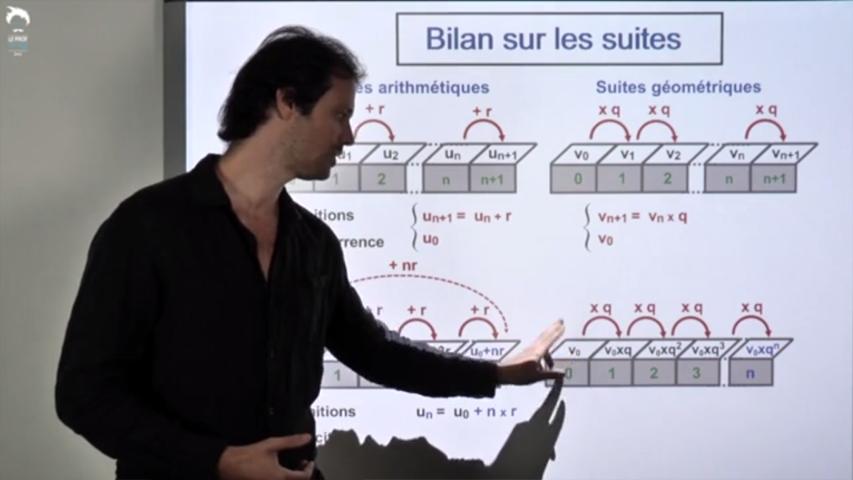
Le cours de première est centré sur deux types de suites plutôt simples : les suites arithmétiques et les suites géométriques.
Elles possèdent des propriétés qu'il faut absolument maîtriser pour s'en sortir dans les problèmes de Terminale.

Le chapitre est découpé en trois parties :
1) Tout ce qu'il faut savoir sur ces deux types de suite.
2) Des problèmes et exercices que tu peux avoir en DS ou DM sur les suites arithmétiques et géométriques.
3) Une ouverture sur l'étude d'autres suites avec quelques exercices eux aussi incontournables.

Enfin, si en classe vous croisez des algorithmes, vous devriez trouver ce que vous cherchez dans ces vidéos.

L'essentiel de ce qu'il faut savoir sur les suites arithmétiques et géométriques. Un bon moyen de commencer sa fiche sur cette leçon !

Grâce à cette vidéo, tu visualiseras les comportements des suites arithmétique ou géométrique.
Un plus pour comprendre l'intégralité du chapitre !

On présente une suite arithmétique dont on essaye de trouver le 101ème terme.
Pour cela on construit successivement sa "définition par récurrence" et sa "définition explicite".
On effectue le même travail sur un deuxième exemple avant d'exposer des formules générales valables pour toutes les suites arithmétiques.
Nous en profitons pour expliquer le vocabulaire rattaché aux suites et une méthode pour les représenter simplement.

On découvre ce qu'est une suite géométrique puis on se donne les mêmes objectifs que dans la vidéo précédente.
- Trouver un terme d'indice donné.
- Donner sa définition par récurrence.
- En déduire sa définition explicite.
Des bases incontournables!

Dans cette vidéo nous allons voir comment traiter deux questions fondamentales sur les suites:
- comment montrer qu'une suite n'est pas arithmétique ou de même n'est pas géométrique ?
- comment retrouver la raison ou le terme initial d'une suite arithmétique ou géométrique dont on ne connait que deux termes ?
Des questions que tu croiseras régulièrement dans les problèmes !